データの代表値を求める際、平均値だけでは実態を正確に把握できないケースがあります。
例えば、社員の給与データで一部の高額所得者が平均を大きく引き上げてしまう場合、平均値は実際の中心的な給与水準を反映しません。
このような場合に有効なのが「中央値」で、データを大きさの順に並べたときの中央に位置する値を示します。
中央値は外れ値の影響を受けにくく、データの典型的な値を知りたい場合に非常に有用です。
Excelには中央値を求めるMEDIAN関数が用意されており、簡単に計算できます。
しかし、実務では「0を除いて計算したい」「特定の条件を満たすデータだけの中央値を求めたい」といった応用的な処理が必要になることも多くあります。
また、中央値と似た概念である最頻値(モード)との違いや使い分けも理解しておく必要があります。
本記事では、MEDIAN関数による基本的な中央値の求め方から、条件付きでの計算方法、0や空白セルを除外する方法、さらには最頻値との違いまで詳しく解説します。
データ分析の精度を高めたい方は、ぜひ最後までお読みください。
ポイントは
・MEDIAN関数で中央値を簡単に求められる
・IF関数や配列数式で条件付き中央値を計算できる
・中央値と平均値・最頻値の違いを理解して使い分けることが重要
です。
それでは詳しく見ていきましょう。
中央値とは?平均値との違いと使い分け
それではまず、中央値の基本的な概念と、平均値との違いを確認していきます。
中央値(メジアン)の基本概念
中央値(メジアン)は、データを小さい順に並べたときに中央に位置する値のことです。
データ数が奇数の場合は真ん中の値、偶数の場合は中央2つの値の平均値が中央値となります。
例えば、5人の年齢データ「25, 30, 35, 40, 50」の場合、中央値は中央に位置する「35」です。
データが「25, 30, 35, 40」の4つなら、中央の2つ「30と35」の平均である「32.5」が中央値になります。
中央値の最大の特徴は、極端に大きい値や小さい値(外れ値)の影響を受けにくいことです。
例えば、「25, 30, 35, 40, 50」というデータの最後の値が「50」ではなく「500」だったとしても、中央値は変わらず「35」のままです。
一方、平均値は大きく変化してしまいます。
このため、所得分布や不動産価格など、極端な値が含まれやすいデータの分析に適しています。
中央値の求め方イメージ
データ数が奇数
25, 30, 35, 40, 50
中央値 = 35
真ん中の値
データ数が偶数
25, 30, 35, 40
中央値 = 32.5
中央2つの平均
平均値と中央値の違い
平均値(算術平均)は、すべてのデータの合計をデータ数で割った値です。
「25, 30, 35, 40, 50」の平均値は「(25+30+35+40+50)÷5=36」となります。
すべてのデータが計算に影響するため、極端な値があると大きく変動します。
例えば、年収のデータで「300万、350万、400万、450万、500万」の5人がいる場合、平均値は400万円、中央値も400万円で一致します。
しかし、1人だけが年収2000万円だった場合、平均値は「(300+350+400+450+2000)÷5=700万円」と大きく上昇しますが、中央値は変わらず400万円のままです。
この場合、実際の典型的な年収水準を示すのは中央値の方です。
| データ | 平均値 | 中央値 | どちらが適切か |
|---|---|---|---|
| 300, 350, 400, 450, 500 | 400万円 | 400万円 | どちらでも同じ |
| 300, 350, 400, 450, 2000 | 700万円 | 400万円 | 中央値が実態を反映 |
| 5, 5, 6, 6, 7 | 5.8 | 6 | どちらも有用 |
中央値を使うべき場面
中央値が特に有効なのは、外れ値が含まれやすいデータや、分布が偏っているデータを分析する場合です。
不動産価格、所得分布、テストの点数(満点や0点が多い場合)、Webサイトの滞在時間(極端に長い値がある場合)などが該当します。
これらのデータでは、平均値が実態とかけ離れた値になりやすく、中央値の方が「典型的な値」を正確に示します。
一方、データが正規分布に近く、外れ値がほとんどない場合は、平均値の方が情報量が多く有用です。
製品の重量、気温の推移、均質な集団の測定値などでは、平均値を使用するのが一般的です。
データの特性を理解し、目的に応じて適切な代表値を選択することが重要です。
統計的には、平均値・中央値・最頻値を合わせて「代表値」と呼びます。
データの分布が左右対称の正規分布の場合、これら3つの値はほぼ一致します。
しかし、分布が偏っている(歪んでいる)場合、それぞれ異なる値を示します。
複数の代表値を比較することで、データの分布の形状や偏りを把握できます。
実務では、平均値と中央値の両方を計算して比較し、データの特性を多角的に理解することが推奨されます。
MEDIAN関数で中央値を求める基本操作
続いては、Excelで中央値を計算する基本的な方法を確認していきます。
MEDIAN関数の基本構文
MEDIAN関数は、「=MEDIAN(数値1,数値2,…)」という構文で、指定した数値の中央値を返します。
引数には、個別のセル参照、セル範囲、または直接数値を指定できます。
例えば、「=MEDIAN(A1:A5)」とすれば、A1からA5までのデータの中央値が計算されます。
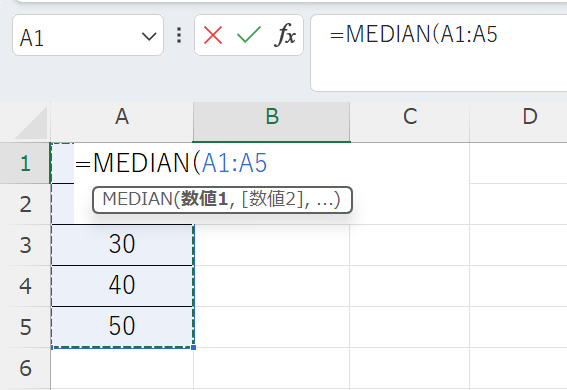
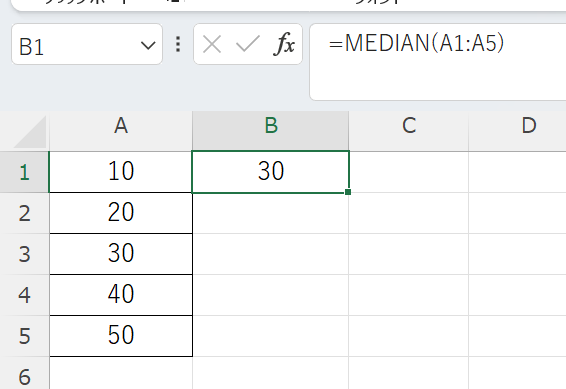
「=MEDIAN(10,20,30,40,50)」のように直接数値を入力することも可能です。
MEDIAN関数は、指定された範囲内の数値だけを自動的に抽出して計算します。
文字列や論理値、空白セルは無視されるため、データに文字が混在していても問題ありません。
ただし、0という数値は計算に含まれるため、0を除外したい場合は別の方法が必要です。
MEDIAN関数の使用例
範囲指定
セル範囲で指定
複数範囲
複数範囲を結合
直接入力
数値を直接指定
| データ(A1:A5) | 数式 | 結果 | 説明 |
|---|---|---|---|
| 10, 20, 30, 40, 50 | =MEDIAN(A1:A5) | 30 | 5つのデータの中央値 |
| 10, 20, 30, 40 | =MEDIAN(A1:A4) | 25 | 中央2つ(20,30)の平均 |
| 5, 10, 15, 20, 100 | =MEDIAN(A1:A5) | 15 | 外れ値の影響を受けない |
空白セルと0の扱い
MEDIAN関数は、空白セルは自動的に無視しますが、0という数値は計算に含まれます。
例えば、「10, 20, 空白, 30, 40」というデータの場合、空白は無視されて「10, 20, 30, 40」の4つで中央値が計算され、結果は25になります。
しかし、「10, 20, 0, 30, 40」の場合、0は数値として扱われ、「0, 10, 20, 30, 40」の5つで計算され、中央値は20になります。
この動作の違いは重要で、特にアンケート結果や測定データで「未入力」と「ゼロという値」を区別したい場合に影響します。
0を除外して計算したい場合は、後述する条件付き中央値の方法を使用する必要があります。
データの性質を理解し、0を含めるべきか除外すべきかを判断することが大切です。
複数の範囲を指定する方法
MEDIAN関数では、カンマで区切って複数の範囲や値を指定できます。
例えば、「=MEDIAN(A1:A5,C1:C5,100)」とすれば、A列とC列の範囲、さらに数値100をすべて含めた中央値が計算されます。
離れた位置にあるデータをまとめて処理する際に便利です。
複数範囲を指定する場合、すべての数値が1つのリストとして扱われます。
A1:A5に「10,20,30」、C1:C5に「40,50,60」が入っている場合、6つの数値「10,20,30,40,50,60」の中央値である「35」が返されます。
範囲の指定順序は結果に影響しません。
MEDIAN関数は、データが既にソート(並び替え)されている必要はありません。
関数が自動的に内部で値を並べ替えて中央値を算出します。
そのため、元のデータの順序を保持したまま中央値を計算できます。
また、MEDIAN関数はエラー値(#DIV/0!、#N/Aなど)が範囲内にあると、エラーを返します。
エラー値を含むデータの場合は、IFERROR関数と組み合わせるか、事前にエラーを処理する必要があります。
条件付きで中央値を求める方法
それでは、特定の条件を満たすデータだけの中央値を求める応用的な方法を確認していきます。
0を除いた中央値の計算
0を除外して中央値を計算するには、IF関数と配列数式を組み合わせる方法が有効です。
「=MEDIAN(IF(A1:A10<>0,A1:A10))」という数式を入力し、Ctrl+Shift+Enterで確定すると配列数式として動作します。
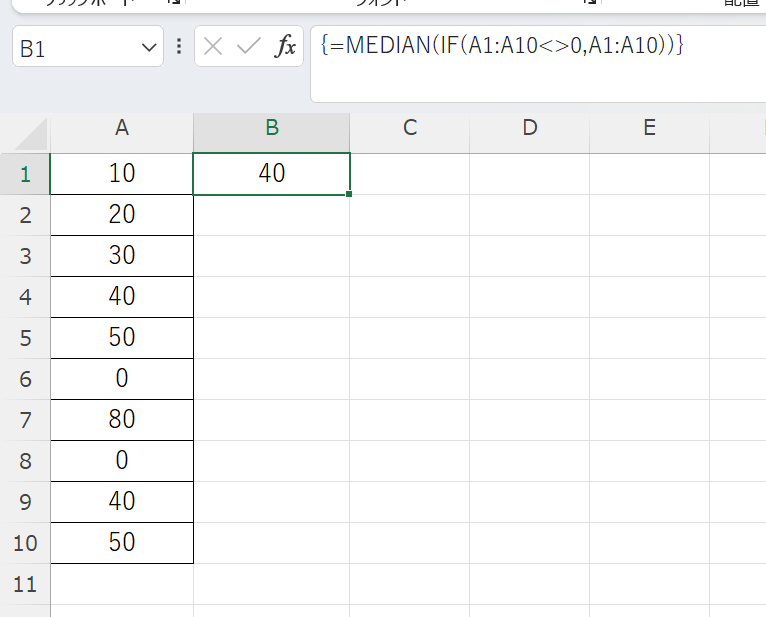
この数式は、A1:A10の範囲で0でない値だけを抽出し、その中央値を計算します。
Excel 365やExcel 2021では、配列数式として自動的に認識されるため、通常通りEnterキーで確定できます。
古いバージョンのExcelでは、必ずCtrl+Shift+Enterで確定する必要があり、数式バーに{=MEDIAN(IF(A1:A10<>0,A1:A10))}のように波括弧が表示されます。
この波括弧は手動で入力するのではなく、Ctrl+Shift+Enterによって自動的に付加されます。
0を除く中央値の計算手順
数式を入力
=MEDIAN(IF(A1:A10<>0,A1:A10))
Ctrl+Shift+Enter
で確定
0を除いた
中央値が表示
| データ | 通常のMEDIAN | 0を除くMEDIAN |
|---|---|---|
| 0, 10, 20, 30, 40 | 20 | 25(10,20,30,40の中央値) |
| 0, 0, 10, 20, 30 | 10 | 20(10,20,30の中央値) |
| 5, 0, 15, 0, 25 | 5 | 15(5,15,25の中央値) |
特定の条件を満たすデータの中央値
より複雑な条件を指定する場合も、IF関数の条件部分を変更することで対応できます。
例えば、50以上の値だけの中央値を求めるなら「=MEDIAN(IF(A1:A10>=50,A1:A10))」とします。
複数の条件を組み合わせることも可能で、「=MEDIAN(IF((A1:A10>0)*(A1:A10<100),A1:A10))」とすれば、0より大きく100未満の値だけの中央値が計算されます。
別の列の条件で絞り込むこともできます。
A列に数値、B列に部署名がある場合、「=MEDIAN(IF(B1:B10=”営業部”,A1:A10))」とすれば、営業部のデータだけの中央値が求められます。
この方法は、SUMIF関数やAVERAGEIF関数のように、条件付き集計を中央値で行いたい場合に非常に便利です。
FILTER関数を使った方法(Excel 365以降)
Excel 365やExcel 2021では、FILTER関数を使ってより直感的に条件付き中央値を計算できます。
「=MEDIAN(FILTER(A1:A10,A1:A10<>0))」という数式で、0を除いた中央値が簡単に求められます。
FILTER関数は条件を満たすデータを抽出する関数で、その結果をMEDIAN関数で処理する構造です。
この方法は配列数式の特殊な入力操作が不要で、通常のEnterキーで確定できます。
また、複数条件も扱いやすく、「=MEDIAN(FILTER(A1:A10,(A1:A10>0)*(A1:A10<100)))」のように記述できます。
Excel 365を使用している場合は、FILTER関数を活用することでより保守性の高い数式を作成できます。
| 方法 | 数式例 | 対応バージョン |
|---|---|---|
| IF配列数式 | =MEDIAN(IF(A1:A10<>0,A1:A10)) | すべてのExcel |
| FILTER関数 | =MEDIAN(FILTER(A1:A10,A1:A10<>0)) | Excel 365以降 |
条件付き中央値は、データのクリーニングや分析において非常に重要です。
アンケート結果で「回答なし」を0として記録している場合、0を除外しないと中央値が実態より低く算出されてしまいます。
また、外れ値を除外して分析したい場合も、条件付き中央値が役立ちます。
データの特性を理解し、適切な条件を設定することで、より正確な分析結果が得られます。
最頻値(モード)との違いと使い分け
最後に、中央値と似た概念である最頻値について、その違いと使い分けを確認していきます。
最頻値(モード)とは
最頻値(モード)は、データの中で最も頻繁に出現する値のことです。
例えば、テストの点数が「50, 60, 70, 70, 70, 80, 90」の場合、最も多く出現する「70」が最頻値となります。
ExcelではMODE.SNGL関数(単一モード)またはMODE.MULT関数(複数モード)で求められます。
MODE.SNGL関数は「=MODE.SNGL(数値1,数値2,…)」という構文で、最も頻度の高い値を1つ返します。
複数の値が同じ頻度で最も多く出現する場合は、最初に見つかった値を返します。
MODE.MULT関数は、同じ頻度で最も多く出現する値がすべて返される配列関数です。
代表値の種類と特徴
平均値
全データの
合計÷個数
中央値
並べた時の
中央の値
最頻値
最も多く
出現する値
| データ | 平均値 | 中央値 | 最頻値 |
|---|---|---|---|
| 10, 20, 30, 30, 30, 40, 50 | 30 | 30 | 30 |
| 10, 20, 30, 30, 100 | 38 | 30 | 30 |
| 5, 5, 10, 15, 15, 20 | 11.7 | 12.5 | 5(または15) |
最頻値を使うべき場面
最頻値は、カテゴリーデータや離散的な値を扱う場合に特に有効です。
靴のサイズ、服のサイズ、好きな色、利用頻度の高い交通手段など、選択肢が限られているデータの分析に適しています。
これらのデータでは、平均値や中央値よりも「最も多くの人が選んだ値」を知ることが重要です。
例えば、靴のサイズのデータが「24.0, 24.5, 25.0, 25.0, 25.0, 25.5, 26.0」の場合、最頻値は「25.0cm」です。
在庫管理では、この最頻値のサイズを多めに仕入れることが合理的です。
平均値「25.0cm」や中央値「25.0cm」も同じ値になりますが、最頻値の概念の方がビジネス判断には直感的です。
中央値・平均値・最頻値の使い分け
データの種類と分析の目的によって、適切な代表値を選択します
。
外れ値が多く影響が大きい場合は中央値、データが正規分布に近く均質な場合は平均値、カテゴリーや離散値で最多の選択を知りたい場合は最頻値が適しています。
実務では、複数の代表値を同時に計算して比較することが推奨されます。
平均値と中央値が大きく異なる場合、データに偏りや外れ値があることがわかります。
3つの代表値がすべて近い値であれば、データが比較的均質であることを示します。
このような多角的な分析により、データの特性を深く理解できます。
| 代表値 | 適した場面 | Excel関数 |
|---|---|---|
| 平均値 | 正規分布、外れ値が少ない | AVERAGE |
| 中央値 | 外れ値あり、偏った分布 | MEDIAN |
| 最頻値 | カテゴリーデータ、離散値 | MODE.SNGL |
統計分析では、「記述統計」としてこれらの代表値をまとめて提示することが一般的です。
Excelのデータ分析ツールを使えば、平均値、中央値、最頻値、標準偏差などを一度に計算できます。
「データ」タブの「データ分析」から「基本統計量」を選択すると、包括的な統計情報が得られます。
データ分析ツールが表示されていない場合は、Excelのオプションからアドインを有効化する必要があります。
まとめ エクセルで中央値の求め方(関数:条件付き:最頻値)
エクセルで中央値を求める方法をまとめると
・MEDIAN関数の基本:「=MEDIAN(数値1,数値2,…)」で中央値を簡単に計算、空白セルは無視されるが0は計算に含まれる、複数範囲をカンマ区切りで指定可能
・条件付き中央値:0を除く場合は「=MEDIAN(IF(A1:A10<>0,A1:A10))」をCtrl+Shift+Enterで配列数式として入力、Excel 365以降では「=MEDIAN(FILTER(A1:A10,A1:A10<>0))」が簡潔
・平均値との違い:中央値は外れ値の影響を受けにくく、偏った分布のデータに適する、所得や不動産価格など極端な値が含まれるデータの分析に有効
・最頻値との使い分け:最頻値は最も頻繁に出現する値で「=MODE.SNGL(範囲)」で計算、カテゴリーデータや離散値の分析に適する、複数の代表値を比較することでデータの特性を把握
中央値は、平均値だけでは見えてこないデータの実態を明らかにする重要な指標です。
特に外れ値が含まれやすいビジネスデータや社会統計データでは、中央値を使うことでより正確な分析が可能になります。
データの特性を理解し、平均値・中央値・最頻値を適切に使い分けることで、分析の精度と説得力が大きく向上します。
条件付き中央値の計算方法をマスターすれば、0や外れ値を除外した分析も自在に行えます。
実務では、複数の代表値を並べて提示することで、データの全体像を多角的に示すことができます。
正確なデータ分析で、的確な意思決定につなげていきましょう!