この記事では、cos(-90°)の値は0?なぜ?求め方・計算方法を解説!について解説していきます。
結論として
といえます
それでは詳しく見ていきましょう。
cos(-90°)の値は0?
それではまず、cos(-90°)の値について解説していきます。
結論からいいますと、
です。
これは三角関数の基本的な性質の一つであり、数学の定理・定義として決まっているためですね。
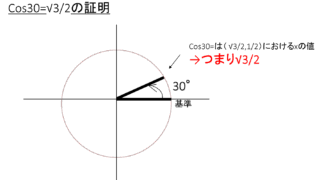
多くの学生が最初に三角関数を学ぶ際、cos0°=1、cos30°=√3/2、cos45°=√2/2、cos60°=1/2といった値を暗記することから始めます
そして、この流れの中でcos(-90°)=0という値も同様に覚えることになります。
cos(-90°)の値がなぜ0になるか?求め方・計算方法の観点から解説
続いては、cos(-90°)の値がなぜ0になるのか?についてを確認していきます。
cos(-90°)が0になる理由を理解するためには、まずコサイン(cosine)の定義を確認するといいです。
コサインには主に2つの定義方法があり、どちらの観点からもcos(-90°)=0であることが証明できます。
単位円による定義とcos(-90°)=0の証明
単位円(半径1の円)において、角度θに対応する点の座標を(x, y)とすると、cosθ=x、sinθ=yとなります。
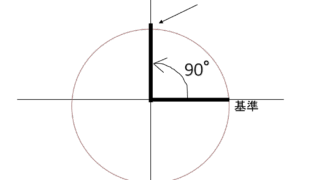
-90°の場合、単位円上の対応する点は(0, -1)となります。
つまり、x座標が0であるため、cos(-90°)=0となるのです。

これは視覚的にも非常に理解しやすく、-90°は真下を向いた方向であり、
水平方向(x軸方向)の成分が全くないことを意味しています。
直角三角形による定義
直角三角形において、cosθ=隣辺/斜辺として定義されます。
しかし、-90°の角度を持つ三角形を考える場合、特殊な状況が発生します。
-90°の角度では、その角に隣接する辺の長さが0に近づきます。
極限的に考えると、隣辺の長さが0となり、cos(-90°)=0/斜辺=0となります。
これらの理由からcos(-90°)は0になるわけです。
特に単位円による理解は直感的で分かりやすく忘れにくいので理解しておきましょう!
まとめ cos(-90°)が0なのはなぜ?求め方・計算方法を解説!
ここでは、cos(-90°)の値は0?なぜ?証明方法・求め方・計算方法を解説!について解説しました。
数学の各知識を身に付けさらに快適な生活を送っていきましょう!