本記事はエクセルにおいて95%信頼区間を求める方法を紹介します。
ポイントは、以下の通りです。
・95%信頼区間:同様の手法で区間を作成した場合、95%の区間が真値を含む範囲
・CONFIDENCE.T関数
・T.INV.2T関数
それでは詳しく確認していきましょう。
区間推定における95%信頼区間とは?
統計的に処理をするにあたって必要な語句を説明します。
統計において母集団とは調査対象全体の集団を言います。
実際にデータを取る時に母集団すべてを網羅するのはなかなか難しいので母集団の中の一部のデータを抽出して母集団に関して推測することが一般的です。
このとき抽出された一部のデータを標本と言います。
例えば、和菓子屋さんで1日に製造されている大福1000個の重量に関して調べます。
しかし、1000個の重量測定はかなりの時間と労力を要するので、1000個の中から無作為に20個を取り出してデータを取ります。
母集団は大福1000個すべて、標本は無作為に取り出した20個となります。
また、以下の語句についても簡単に紹介します。
母平均:母集団における平均
母比率:母集団の中である性質をもつ個体の割合
標本平均:標本における平均
標本比率:標本の中である性質をもつ個体の割合
区間推定は母集団の真値が含まれると思われる範囲を推定する方法です。(真値:母平均、母比率など)
考えられる範囲を信頼区間といいます。
95%信頼区間は母集団から標本を取って、その平均から信頼区間を求める手法を用いた場合、同様の手法で作成された100個の区間のうち、95個の区間が真値を含むことを意味します。
エクセルで95%信頼区間の計算方法1
大福20個の重量を測定したデータです。
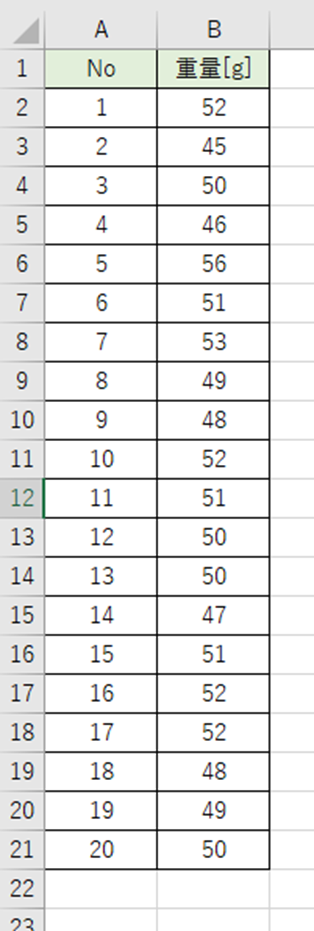
このデータから平均値の95%信頼区間を出します。
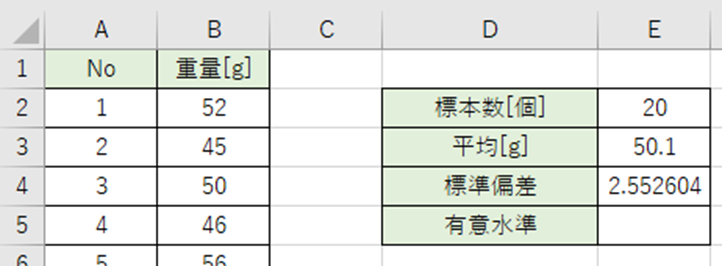
必要な統計量をまとめます。
標本数は調査・実験で抽出された標本の数です。
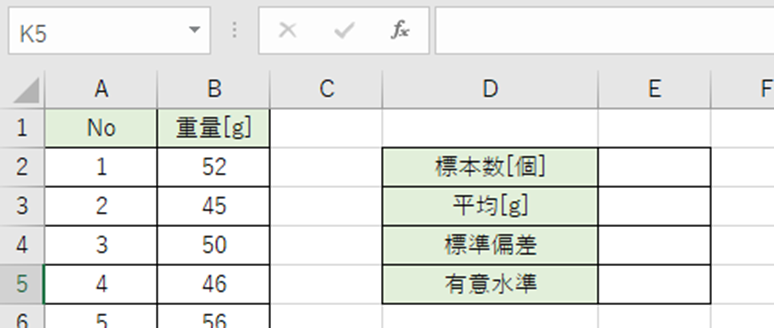
今回はサンプルが20個よりE2セルに20を入力。
平均値はデータの合計をデータの個数で割ったものです。
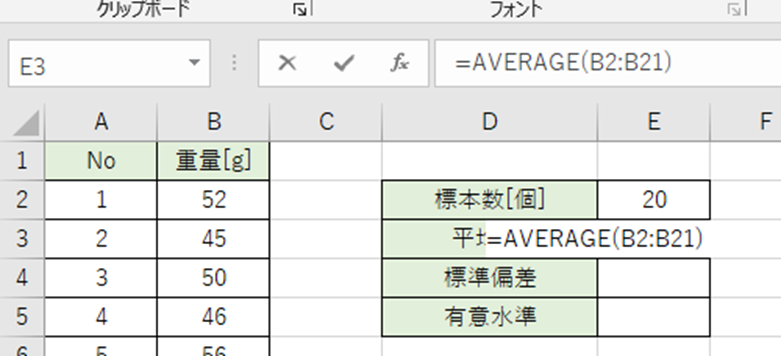
平均値はAVERAGE関数で出します。
以下の数式をE3セルに入力。
=AVERAGE(B2:B21)
標準偏差はデータのばらつきを表す統計量です。平均値の周辺でどれくらいばらついているかを示します。
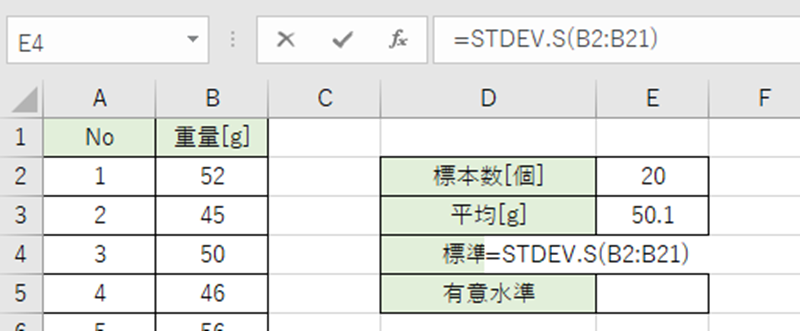
標準偏差はSTDEV.S関数で出します。
以下の数式をE4セルに入力。
=STDEV.S(B2:B21)
有意水準は仮説検定をする際に仮説を棄却するか判断する為の基準を言います。
ここで仮説検定とはデータからある仮説が正しいか判断する手法です。
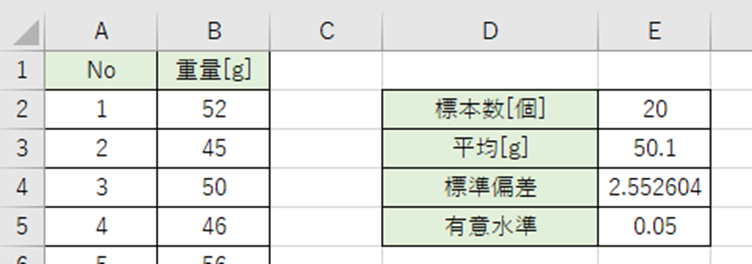
95%信頼区間ということなので有意水準は
1-0.95=0.05
以下の数式をE5セルに入力。
=0.05
信頼区間を出します。
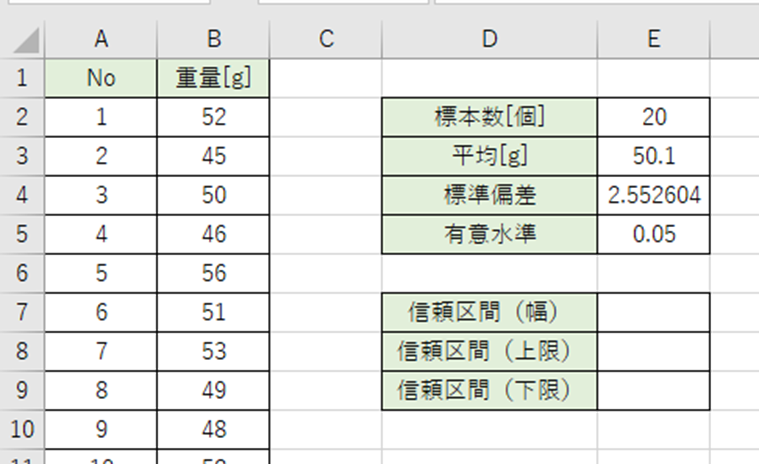
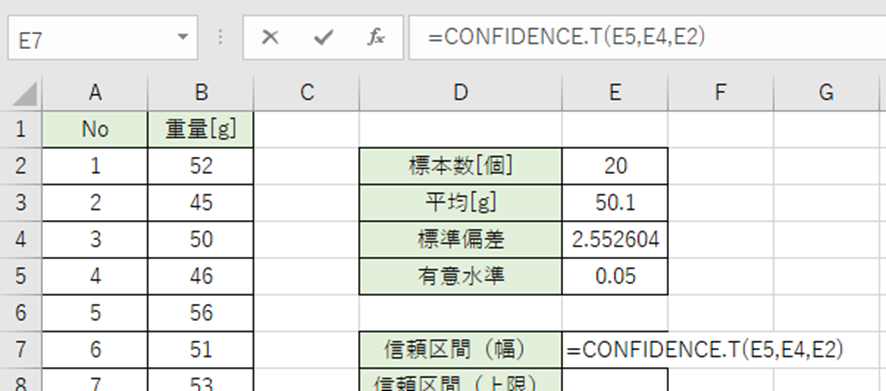
CONFIDENCE.T関数で信頼区間の幅を出します。
CONFIDENCE.T(有意水準α,標準偏差,標本数)
以下の数式をE7セルに入力。
=CONFIDENCE.T(E5,E4,E2)
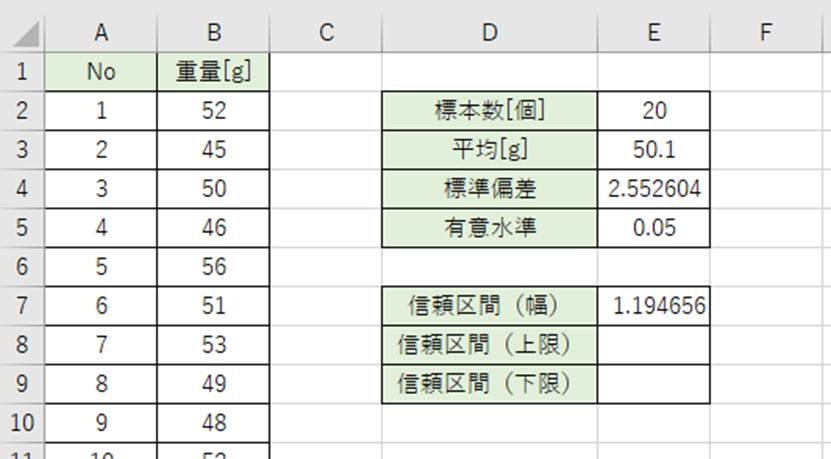
平均+信頼区間の幅=信頼区間の上限
以下の数式をE7セルに入力。
=E3+E7
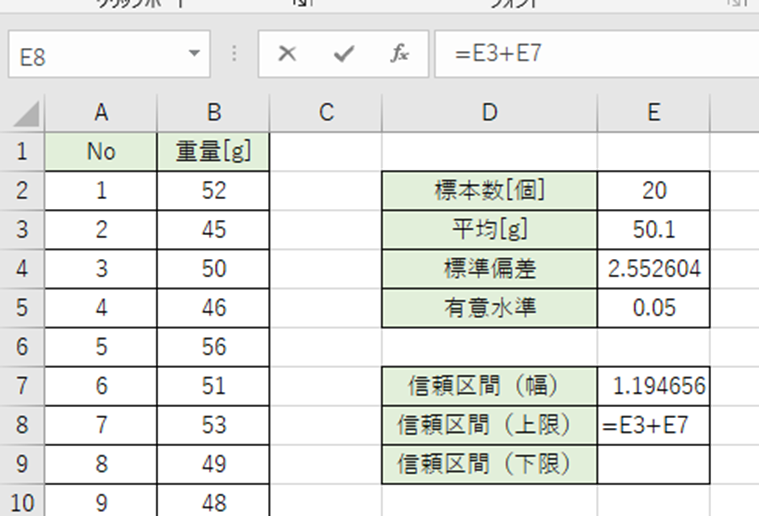
平均-信頼区間の幅=信頼区間の下限
以下の数式をE8セルに入力。
=E3-E7
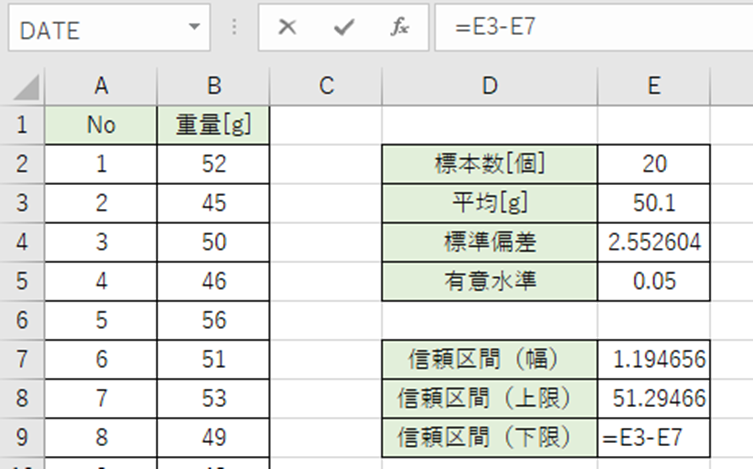
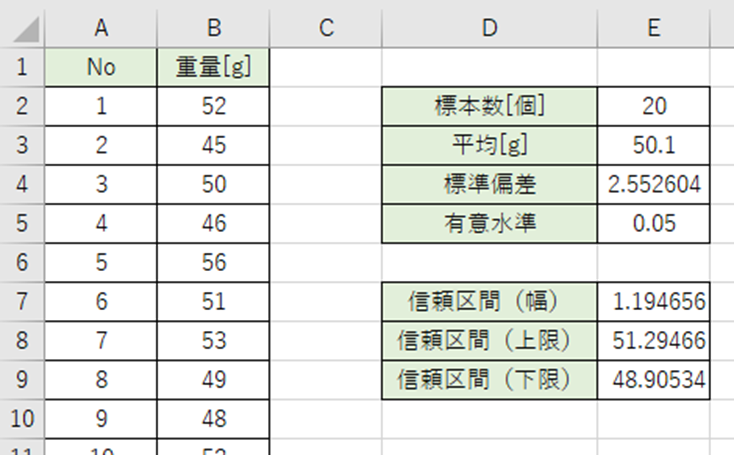
この標本で平均重量の95%信頼区間は48.9~51.3g です。
エクセルで95%信頼区間の計算方法2
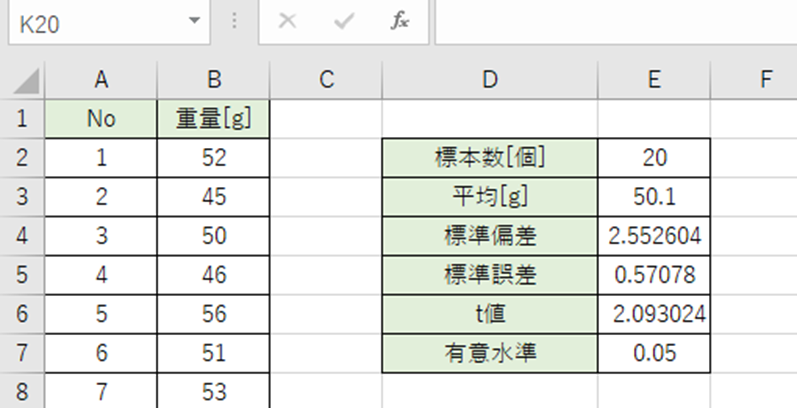
次に統計量の表に標準誤差とt値を追加します。
標準誤差とt値から95%信頼区間を出します。
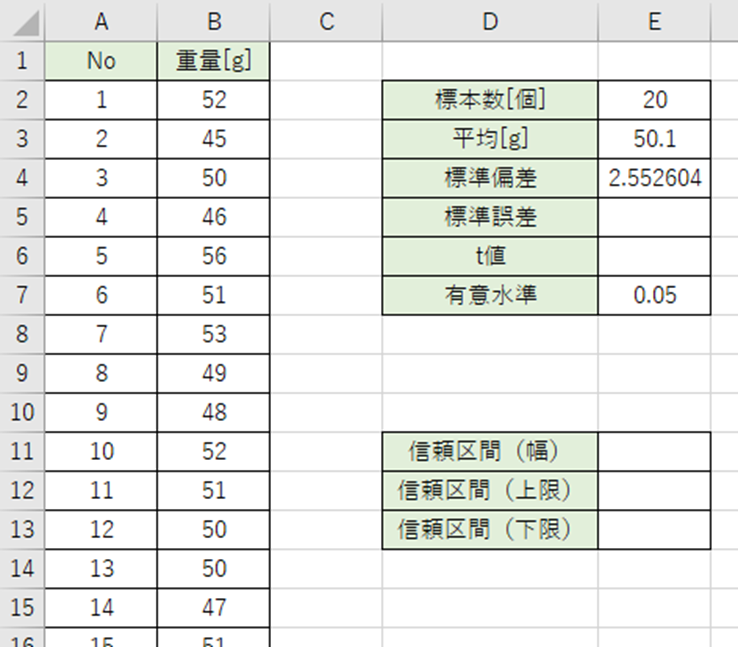
標準誤差とは標本から得られる推定量のばらつきです。
標準偏差を標本数の平方根で割ると出ます。
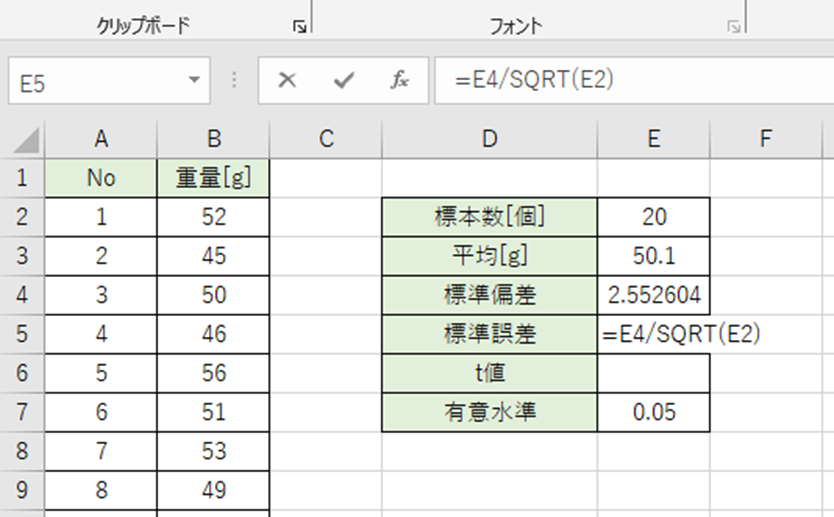
以下の数式をF2セルに入力。
=E4/SQRT(E2)
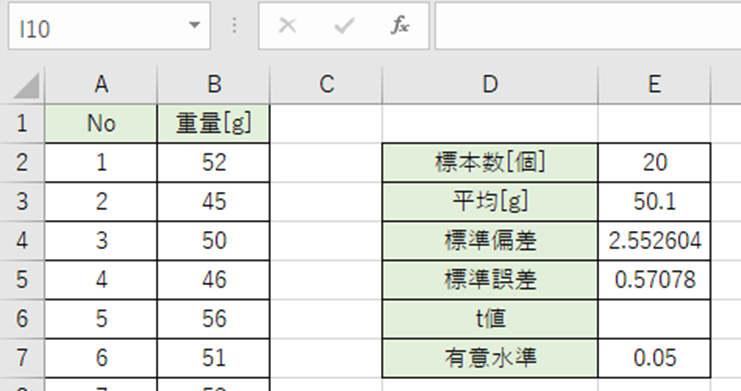
t値はt分布に基づく統計量です。
ここでt分布とは母集団の標準偏差が分からない場合、母平均の推定に使用される確率分布です。
T.INV.2T関数で出します。
=T.INV.2T(有意水準α,自由度)
自由度とは自由に決めることができる値の数のことです。
今回は自由度は標本数-1です。
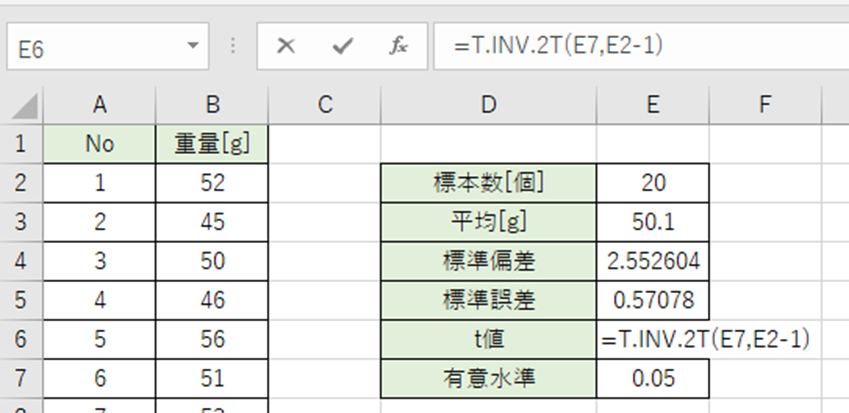
以下の数式をF3セルに入力。
=T.INV.2T(E5,E2-1)
信頼区間を求めます。
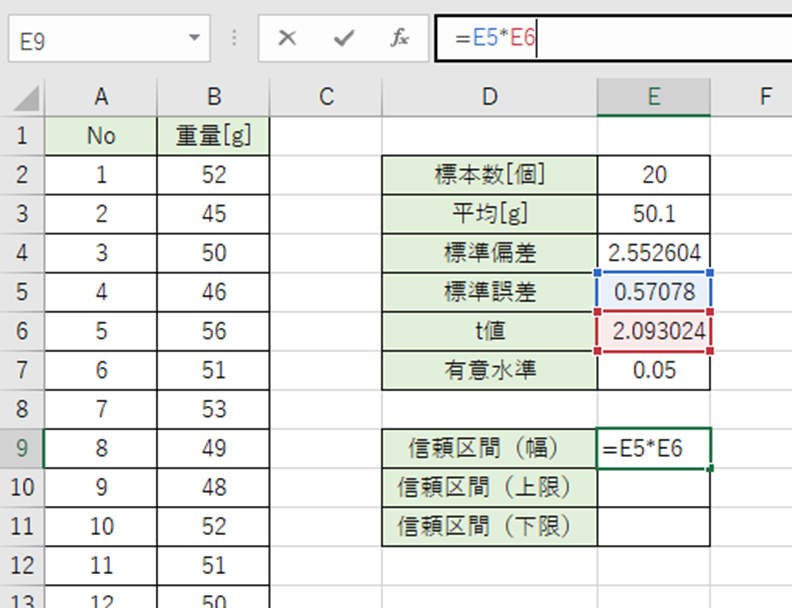
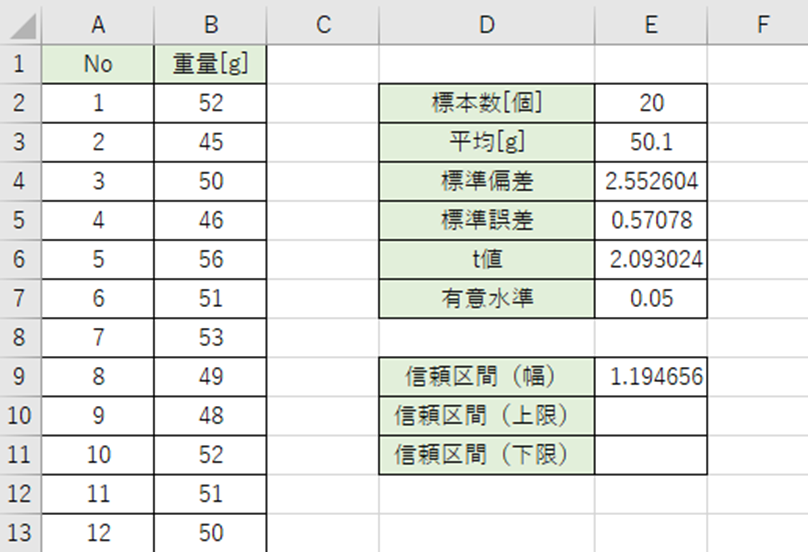
信頼区間の幅は標準誤差とt値をかけると出ます。
以下の数式をE9セルに入力。
=E5*E6
同様に信頼区間の上限と下限は平均値に信頼区間の幅を足すまたは引くと求められます。
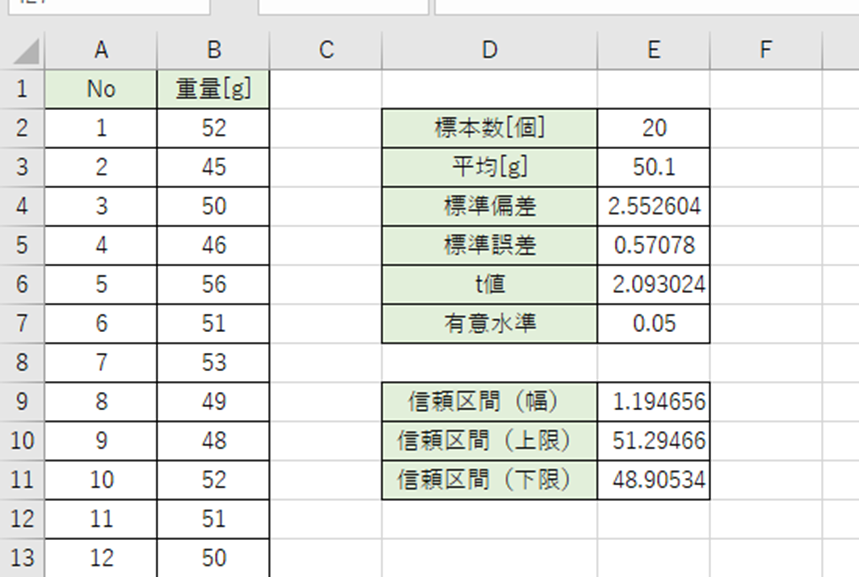
この標本で平均重量 95%信頼区間は48.9~51.3g です。
まとめ エクセルで95%信頼区間を求める方法
この記事では、エクセルで95%信頼区間を求める方法について紹介しました。
エクセルにて簡単に信頼区間を出すことができ、便利なのでぜひ活用してみてください。